Mathe ist ein gefährlicher Cocktail:
Don't Drink And Derive!
Die ultimatiefste Mathe-Witzesammlung

Genesis der Mathematik

  1. Am Anfang schuf Gott Adam und Eva. Und Adam war wüst und leer, und es wollte nicht Licht werden im Kasten seines Gehirns, wo Finsternis und Chaos herrschten. Und Gott sprach: "Es werde eine Feste in der Wirre der Gedanken und Begriffe und ihr Name sei Mathematik." Und es geschah also. So ward aus plus und minus der erste Tag.

  2. Und Gott schuf gerade und krumme Linien, ebene und gewölbte Flächen und Körper der verschiedensten geometrischen Formen mit Winkeln und Längen und gab sie Adam, auf daß er sie berechne und sich an ihnen erfreue. Und Gott sah, daß es gut war. So ward aus Sinus und Kosinus der zweite Tag.

  3. Und Gott schuf Potenzen und Wurzeln, rein- und gemischtquadratische Gleichungen, reelle und imaginäre Zahlen und sprach zu Adam: "Rechne mit ihnen nach den Gesetzen der Algebra und du wirst den binomischen Lehrsatz finden." So ward aus Quadrat und Kubik der dritte Tag.

  4. Und Gott sprach: "Es werde das Koordinatensystem mit seinem Ursprung, mit Ordinate und Abszisse. In dieses sollen sich einfügen Kreise, Ellipsen, Hyperbeln mit Pol, Polaren, konjugierten Durchmessern und Tangenten, Kurven höherer und noch höherer Ordnung, Asymptoten, Hoch- und Tiefpunkten, mit und ohne Wendepunkten." Und Gott sah, daß es gut war. So ward aus Maximum und Minimum der vierte Tag.

  5. Und Gott formte die Erde mit Groß- und Kleinkreisen, mit Längen- und Breitenkreisen, mit Meridianen und Vertikalen und gab ihr einen Platz im Mittelpunkt der Himmelskugel mit Horizont, Zenit und Nadir, mit Äquator, Nord- und Südpol, und er setzte auf diese Kugel Gestirne, deren Lage durch Höhe, Deklination und Stundenwinkel bestimmt war. Und Gott betrachtete sein Werk mit Wohlgefallen. So ward aus Längenzeit und Zeitgleichung der fünfte Tag.

  6. Und Gott sprach: "Die Erde bringe hervor kleine und kleinste Teilchen in einer Menge, daß ihre Zahl gegen unendlich strebe." Und es geschah also. Und der Herr nannte diese Teilchen lim x für x gegen unendlich. Er schuf die Herren Briggs und Napier, auf daß sie Logarithmen schufen, und er baute Reihen, endliche und unendliche. Da ward aus konvergent und divergent der sechste Tag.

  7. Am siebten Tage aber ruhte Gott. Und er gab Adam die Logarithmentafel und sprach: "Siehe ich gebe in Deine Hände das ganze mathematische Paradies. Nun darfst du addieren und multiplizieren und potenzieren. Nur durch die Zahl 0 darfst du nicht dividieren; denn diese Zahl ist ein Geschöpf des Fürsten der Finsternis."

  8. Die listige Schlange aber sprach zu Eva: "Wer durch 0 dividiert, wird lernen, was richtig und falsch ist." Und das törichte Weib sprach zu Adam: "Dividiere und die Gleichung wird viel einfacher werden."

  9. Und Adam faßte sich ein Herz und dividierte durch 0. Da wurden ihre Augen aufgetan, und sie erkannten, daß sie nackt waren. So machten sie sich Schürzen aus abgewickelten Oberflächenintegralen. Da trieb Gott Adam und Eva aus dem mathematischen Paradies und sprach zu ihnen: "Weil Du durch 0 dividiert hast, sei deine Arbeit verflucht. Im Schweiße deines Angesichts sollst du dein Leben lang differenzieren, integrieren und logarithmieren. Nie sollst du eine Zahl unendlich erreichen und für p und e genaue Werte finden. Du wirst für den Sinus von zwei verschiedenen Zahlen den gleichen Wert erhalten und nie einen exakten mathematischen Text hervorbringen."

    Und so geschah es also.

Mathematische Unterhaltungen

(Mathematische) Elefantenjagd

Wie man einen Löwen in der Wüste fängt

  1. Die HILBERTsche oder axiomatische Methode. Man stellt einen Käfig in die Wüste und führt folgendes Axiomensystem ein:
    Axiom 1: Die Menge der Löwen in der Wüste ist nicht leer.
    Axiom 2: Sind Löwen in der Wüste, so ist auch ein Löwe im Käfig.
    Schlußregel: Ist p ein richtiger Satz, und gilt „Wenn p, so q“, so ist auch q ein richtiger Satz.
    Satz:Es ist ein Löwe im Käfig.

  2. Die geometrische Methode. Man stelle einen zylindrischen Käfig in die Wüste.
    1. Fall: Der Löwe ist im Käfig. Dieser Fall ist trivial!
    2. Fall: Der Löwe ist außerhalb des Käfigs. Dann stell man sich in den Käfig und mache eine Inversion an den Käfigwänden. Auf diese Art und Weise gelangt der Löwe in den Käfig und man selbst nach draußen.
    Achtung: Bei Anwendung dieser Methode ist darauf zu achten, daß man sich nicht in die Mitte des Käfigbodens stellt, da man sonst im Unendlichen verschwindet!

  3. Die Projektionsmethode. Ohne Beschränkung der Allgemeinheit nehmen wir an, daß die Wüste eine Ebene ist. Wir projezieren sie auf eine Gerade durch den Käfig, und die Gerade auf einen Punkt im Käfig. Damit gelangt der Löwe in den Käfig.

  4. Die BOLZANO-WEIERSTRASS-Methode. Wir halbieren die Wüste in Nord-Süd-Richtung durch einen Zaun. Dann ist der Löwe entweder in der westlichen Hälfte oder östlichen Hälfte. Wir wollen annehmen, daß er in der westlichen Hälfte ist. Daraufhin halbieren wir diesen westlichen Teil durch einen Zaun in Ost-West-Richtung. Der Löwe ist entweder im nördlichen oder im südlichen Teil. Wir nehmen an, er ist im nördlichen. Auf diese Weise fahren wir fort. Der Durchmesser der Teile, die bei der Halbiererei entstehen, strebt gegen Null. Auf diese Weise wird der Löwe schließlich von einem Zaun beliebig kleiner Länge eingegrenzt.

  5. Die mengentheoretische Methode. Die Punkte in der Wüste lassen sich wohlordnen. Ausgehend vom kleinsten Element erwischt man den Löwen durch transfinite Induktion.
    Bemerkung: Diese Methode ist in Fachkreisen umstritten wegen der Verwendung des Wohlordnungssatzes bzw. des Auwahlaxioms. Wie so oft, hat auch die vorliegende Fragestellung zu einer fruchtbaren Entwicklung geführt. Dabei wurde schließlich eine sehr viel einfachere Methode entdeckt, die den genannten Mangel nicht aufweist: Man betrachte alle Teilmengen der Wüste, die den Löwen enthalten und bilde ihren Durchschnitt. Er enhält als einziges den Löwen.

    Bei dieser Durchschneiderei sollte lediglich darauf geachtet werden, daß das schöne Fell des Löwen nicht zerschnitten wird!

  6. Die funktionalanalytische Methode. Die Wüste ist ein separabler Raum. Er enthält daher eine abzählbare dichte Menge, aus der eine Folge ausgewählt werden kann, die gegen den Löwen konvergiert. Mit einem Käfig auf dem Rücken springen wir von Punkt zu Punkt dieser Folge und nähern uns so dem Löwen beliebig genau.

  7. Die PEANO-Methode. Man konstruiere eine PEANO-Kurve durch die Wüste, also eine stetige Kurve, die durch jeden Punkt der Wüste geht. Es ist gezeigt worden, daß man eine solche Kurve in beliebig kurzer Zeit durchlaufen kann. Mit dem Käfig unterm Arm durchlaufe man die Kurve in kürzerer Zeit, als der Löwe benötigt, um sich um seine eigene Länge fortzubewegen.

  8. Die topologische Methode Der Löwe kann topologisch als Torus aufgefaßt werden. Man transportiere die Wüste in den vierdimensionalen Raum. Es ist nun möglich die Wüste so zu deformieren, daß beim Rücktransport in den dreidimensionalen Raum der Löwe verknotet ist. Dann ist er hilflos.

  9. Die Kompaktheitsmethode. Die Wüste wird ohne Beschränkung der Allgemeinheit als kompakt vorausgesetzt. Man überdecke sie mit einer Familie von Käfigen Ki (i aus I). Dann gibt es unter ihnen endlich viele Käfige, Ki1, ... ,in , die bereits die ganze Wüste überdecken. Die Durchmusterung dieser Käfige wird als Diplomarbeit vergeben.

  10. Die logische Methode oder die Methode des tertium non datur. Man stelle einen offenen Käfig in die Wüste und lege ein Brett mit Leim daneben. Beides biete man dem Löwen zum Betreten an. Der Löwe sagt dann: „Nein, auf den Leim gehe ich nicht!“ Nach dem tertium non datur muß er in den Käfig gehen. Danach schlägt man die Tür zu.

  11. Die stochastische Methode. Man benötigt dazu ein LAPLACE-Rad, einige Würfel und eine GAUSSe Glocke. Mit dem LAPLACE-Rad fährt man in die Wüste und wirft mit den Würfeln nach dem Löwen. Kommt er dann wutschnaubend angerannt, so stülpt man die Gaußsche Glocke über ihn. Unter ihr ist er mit der Wahrscheinlichkeit eins gefangen.

  12. Die didaktische Methode. Man nähere sich dem Löwen auf der Brunnerschen Spirale. Dann elementarisiere man den Löwen zu einer Katze und fange ihn mit einer Schale Milch.

  13. Die Fixpunktmethode. Es sei f eine Kontraktion der Wüste in sich mit Fixpunkt. Auf diesen Fixpunkt stellen wir den Käfig. Durch sukzessive Iteration W(n+1) = f(W(n)), n=0,1,2,... (W(0)=Wüste) wird die Wüste auf den Fixpunkt zusammengezogen. So gelangt der Löwe in den Käfig.

  14. Die Abstandsmethode. Wir stellen einen Käfig in die Wüste, verlassen diese unauffällig und definieren in ihr die indiskrete Metrik, d.h. der Abstand zwischen allen Punkten ist 0. Insbesondere ist also der Abstand zwischen Löwe und Käfig gleich Null, d.h. der Löwe ist im Käfig.

  15. Die Methode der vollständigen Induktion. Ein Löwe sei in der Wüste. Mit vollständiger Induktion zeigt man leicht, daß für beliebige n aus N gilt: n Löwen sind in der Wüste. Weil die Wüste endlichdimensional (dim W = 3) ist, liegen die Löwen für hinreichend große n überall dermaßen dicht, daß zwangsläufig einer in den Käfig gedrängt wird.
PHYSIKALISCHE METHODEN:

  1. Die NEWTONsche Methode. Käfig und Löwe ziehen sich durch die Gravitationskraft an. Wir vernachlässigen die Reibung. Auf diese Weise muss der Löwe früher oder später im Käfig landen.

  2. Die HEISENBERG-Methode. Ort und Geschwindigkeit eines bewegten Löwen lassen sich nicht gleichzeitig bestimmen. Da bewegte Löwen also keinen physikalisch sinnvollen Ort einnehmen, kommen sie für die Jagd auch nicht in Frage. Die Löwenjagd kann sich daher nur auf ruhende Löwen beschränken. Das Einfangen eines ruhenden, bewegungslosen Löwen wird dem Leser als übungsaufgabe überlassen.

  3. Die SCHRÖDINGER-Methode. Die Wahrscheinlichkeit dafür, daß sich ein Löwe zu einem beliebigen Zeitpunkt im Käfig befindet ist größer als Null. Man setze sich vor den Käfig und warte.

    Bemerkung: Hierbei wird üblicherweise vorausgesetzt, daß der Käfig offen ist und man ihn zuschlagen muß, wenn der Löwe drin ist. Schubert wies aber darauf hin, daß man den Käfig wegen des Tunneleffekts auch zulassen kann. Auf diese Weise kann man bei der elenden Warterei auch mal weggehen und ein Bierchen trinken. Aber nicht zu lange! Denn kluge Löwen, die den Tunneleffekt begriffen haben, verschwinden auch wieder.

  4. Die EINSTEINsche oder relativistische Methode.
    Man überfliege die Wüste nahezu mit Lichtgeschwindigkeit. Durch die relativistische Längenkontraktion wird der Löwe flach wie Papier. Man greife ihn, rolle ihn auf, und mache ein Gummiband herum.

    Um dem Existensproblem zu entgehen, hier noch ein letzter:

  5. Die dialektische Methode. Man zäunt die Wüste ein, bewässert sie, sät Gras und setzt Kaninchen aus. Die Kaninchen vermehren sich schnell. Nach HEGEL kommt daher bald der Zeitpunkt, bei dem Quantität in Qualität umschlägt, und dann hat man einen Löwen.

Der Blabla-Operator

Der Blabla Operator wird seit alters her in allen Bereichen der Wissenschaft mit größtem Erfolg angewendet; erst im letzten Drittel des 20. Jahrhunderts wurde er vorn Verfasser auf eine exakte mathematische Grundlage gestellt. Wegen seiner fundamentalen Bedeutung sollen seine wichtigsten Eigenschaften hier zusammengestellt werden.

Notation. Das Symbol für den Blabla Operator ist die stilisierte Sprechblase: .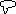

Definitionsbereich. Der Blabla Operator 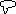wirkt im gesamten Phrasenraum, er ist nach oben unbeschränkt.

Lorentzinvarianz. Der Blabla Operator 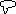kommutiert mit allen Generatoren der Lorentzgruppe: [Pmn, 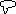]= 0, er ist daher in jedem Koordinatensystem anwendbar.

Opportunität. Sei A eine Aussage, B deren Negation. Dann kann man durch Anwendung von 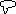sowohl A als auch B beweisen, in Formeln: = -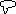

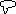
Iteration. 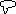kann beliebig oft hintereinander angewandt werden, verliert dabei allerdings zunehmend an Wirkung; exakt formuliert:


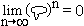
(im Sinne der starken Konversation im Phrasenraum).

Spektralsatz. Die Eigenwerte des Blabla-Operators bestehen aus den zur jeweiligen Zeit vorliegenden experimentellen Daten sowie einem Kontinuum von Vorhersagen.

Dies sind die wichtigsten Eigenschaften, die für die meisten Anwendungen völlig ausreichen. Um mit dem -Operator besser vertraut zu werden, sei die Bearbeitung der folgenden Übungen empfohlen.

1) Berechne den Blabla-Operator in Polarkoordinaten und leite daraus alle wichtigen Eigenschaften der Kugelfunktionen ab. (3 Punkte)
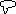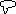2) Beweise die Gleichung = 1 / . Was bedeutet sie physikalisch? (2 Punkte)
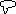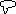3) In der Vorlesung war der Blabla Operator ausführlich auf das Wasserstoffatom angewandt worden. Zeige wie er im Limes p->0 in den Blabla-Operator der klassischen Mechanik übergeht und löse damit das Keplerproblem. (3 Punkte)

Top Ten excuses for not doing Maths homework

  1. I accidentally divided by zero and my paper burst into flames.
  2. Isaac Newton's birthday.
  3. I could only get arbitrarily close to my textbook. I couldn't actually reach it.
  4. I have the proof, but there isn't room to write it in this margin.
  5. I was watching the World Series and got tied up trying to prove that it converged.
  6. I have a solar powered calculator and it was cloudy.
  7. I locked the paper in my trunk but a four-dimensional dog got in and ate it.
  8. I couldn't figure out whether i am the square of negative one or i is the square root of negative one.
  9. I took time out to snack a doughnut and a cup of coffee. I spent the rest of the night trying to figure which one to dunk.
  10. I could have sworn I put the homework inside a Klein bottle, but this morning I couldn't find it.

Some like it in English...

Mathematics Glossary

Any student who ever sat or slept trough a mathematics course knows that certain words and phrases occur very frequently. This glossary might eliminate some confusion.

The instructor saysHe really means
trivialThe student might be able to do it in three hours or so.
simpleAn "A" student can do it in a week or so.
easyThis topic would make a good master's thesis.
clearThe instructor can do it (he thinks).
obviousThe instructor is sure it is in his notes somewhere.
certainlyThe instructor saw one of his instructors do it, but has completely forgotten how it was done.
left as an exercise for the studentThe instructor lost his notes.
is well knownThe instructor heard that someone once did it.
can be shownThe instructor thinks it might be true, but has no idea how to prove it.
the diligent student can showIt is an unsolved problem - probably harder than FERMAT's Last Theorem.

What is a Mathematician?

It is important for people (especially students) to understand what a mathematician is and what s/he does. The little comparison below says a lot.

  • The biologist says "I study the principles of life."
  • The psychologist says "You are controlled by the principles of life."
  • The businessman says "My business can use its force to control the economy."
  • The economist says "The forces of the economy will control your business."
  • The engineer says "My equations are a model of the universe."
  • The physicist says "The universe is a model of my equations."
  • The mathematician says "I don't care."

    • Noah and the Logarithms

    As everyone knows, Noah built an arc. Here is some additional information about what happened when the animals were getting off...

    Now, the world was pretty well empty of land creatures, so Noah gave all of the animals instructions as they departed.
    To the Aardvarks, he commanded, "Go forth and multiply!"
    A couple snakes came slithering out, and he commanded, "Go forth and multiply!"
    "We can't, we're adders." replied the snakes.
    Well Noah kept giving commands, until at last he told the zebras, "Go forth and multiply!"
    A while later he was walking around and stepped over a fallen tree.
    There were those snakes, well, er... multiplying.
    "I thought you said you couldn't multiply?" asked Noah.
    "By logs we can!" replied the adders.

    All Odd Integers Higher Than 2 Are Prime.

    Several students were asked the following problem: Prove that all odd integers higher than 2 are prime.
    Feedback für diese Seite ist erwünscht! Was findest Du gut, schlecht, miserabel? Was fehlt, gehört ergänzt, weggelassen?
    Übersicht
    Mathewitze
    Physikwitze
    © 1997-2000 Robert Wagner, 08/01/97, 08/14/98, 08/15/00